GNU Octaveで2次系のボード線図

GNU Octave（MATLAB互換の数値解析ソフト）で2次系のボード線図を求めてみる。

ボード線図は、以下の関数を用いる。
[MAG, PHASE, W] = bode (SYS, W, OUT_IDX, IN_IDX)
伝達関数は、以下の関数を用いる。
tf (NUM, DEN, TSAM, INNAME, OUTNAME)

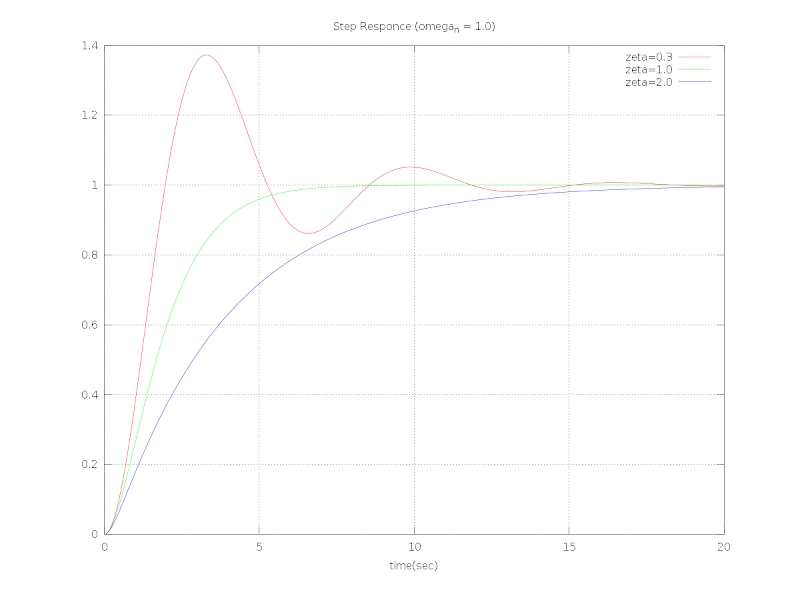
①ζ=0.3, 1.0, 2.0 (ωn=1.0)のとき

%2次系のボード線図,ζ依存性
clf

%ωn=1.0,ζ=0.3,ω=10^-2～10^2,データ数=1000のとき
[mag,pha,frq]=bode(tf([1.0^2],[1 2*0.3*1.0 1.0^2]),logspace(-2,2,1000));

subplot(2,1,1);
semilogx(frq,20*log10(mag),"1")
legend("zeta=0.3")
hold on;

subplot(2,1,2);
semilogx(frq,pha,"1")
legend("zeta=0.3")
hold on;

%ωn=1.0,ζ=1.0,ω=10^-2～10^2,データ数=1000のとき
[mag,pha,frq]=bode(tf([1.0^2],[1 2*1.0*1.0 1.0^2]),logspace(-2,2,1000));

subplot(2,1,1);
semilogx(frq,20*log10(mag),"2")
legend("zeta=1.0")
hold on;

subplot(2,1,2);
semilogx(frq,pha,"2")
legend("zeta=1.0")
hold on;

%ωn=1.0,ζ=2.0,ω=10^-2～10^2,データ数=1000のとき
[mag,pha,frq]=bode(tf([1.0^2],[1 2*2.0*1.0 1.0^2]),logspace(-2,2,1000));

subplot(2,1,1);
semilogx(frq,20*log10(mag),"3")
legend("zeta=2.0")
hold on;

subplot(2,1,2);
semilogx(frq,pha,"3")
legend("zeta=2.0")
hold on;

%x軸=10E-2～10E+2,y軸=-100～20
subplot(2,1,1);
axis([10^-2 10^2 -100 20])
xlabel("omega(rad/sec)")
ylabel("gain(dB)")
title("bode plot (omega_n = 1.0)")
grid;

%x軸=10E-2～10E+2,y軸=-180～0
subplot(2,1,2);
axis([10^-2 10^2 -180 0])
xlabel("omega(rad/sec)")
ylabel("phase(deg)")
grid;

%pngファイルに保存
print -dpng bode1.png



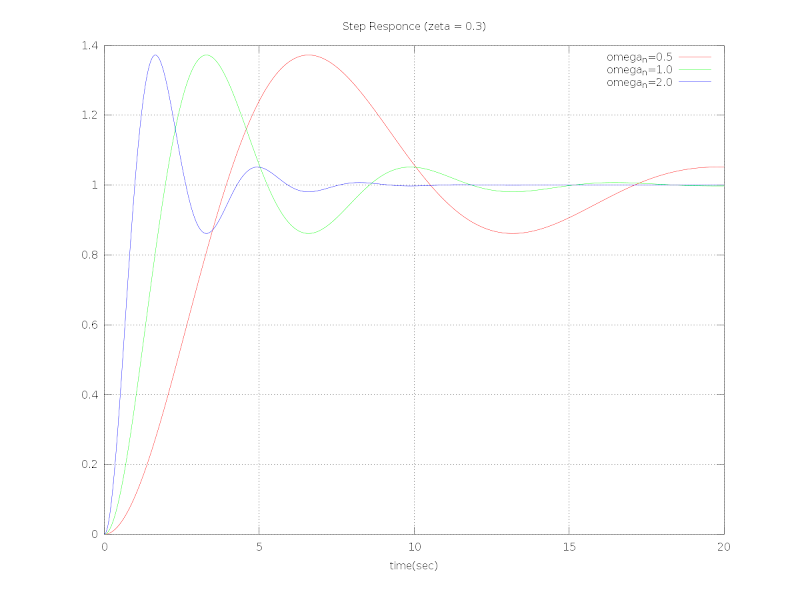
②ωn=0.5, 1.0, 2.0 (ζ=0.3)のとき、

%2次系のボード線図,ωn依存性
clf

%ωn=0.5,ζ=0.3,ω=10^-2～10^2,データ数=1000のとき
[mag,pha,frq]=bode(tf([0.5^2],[1 2*0.3*0.5 0.5^2]),logspace(-2,2,1000));

subplot(2,1,1);
semilogx(frq,20*log10(mag),"1")
legend("omega_n=0.5")
hold on;

subplot(2,1,2);
semilogx(frq,pha,"1")
legend("omega_n=0.5")
hold on;

%ωn=1.0,ζ=0.3,ω=10^-2～10^2,データ数=1000のとき
[mag,pha,frq]=bode(tf([1.0^2],[1 2*0.3*1.0 1.0^2]),logspace(-2,2,1000));

subplot(2,1,1);
semilogx(frq,20*log10(mag),"2")
legend("omega_n=1.0")
hold on;

subplot(2,1,2);
semilogx(frq,pha,"2")
legend("omega_n=1.0")
hold on;

%ωn=2.0,ζ=0.3,ω=10^-2～10^2,データ数=1000のとき
[mag,pha,frq]=bode(tf([2.0^2],[1 2*0.3*2.0 2.0^2]),logspace(-2,2,1000));

subplot(2,1,1);
semilogx(frq,20*log10(mag),"3")
legend("omega_n=0.2")
hold on;

subplot(2,1,2);
semilogx(frq,pha,"3")
legend("omega_n=0.2")
hold on;

%x軸=10E-2～10E+2,y軸=-100～20
subplot(2,1,1);
axis([10^-2 10^2 -100 20])
xlabel("omega(rad/sec)")
ylabel("gain(dB)")
title("bode plot (zeta = 0.3)")
grid;

%x軸=10E-2～10E+2,y軸=-180～0
subplot(2,1,2);
axis([10^-2 10^2 -180 0])
xlabel("omega(rad/sec)")
ylabel("phase(deg)")
grid;

%pngファイルに保存
print -dpng bode2.png

GNU Octaveで2次系のステップ応答

GNU Octave（MATLAB互換の数値解析ソフト）で2次系のステップ応答ステップ応答を求めてみる。

ステップ応答は、以下の関数を用いる。
[Y, T] = step (SYS, INP, TSTOP, N)
伝達関数は、以下の関数を用いる。
tf (NUM, DEN, TSAM, INNAME, OUTNAME)

①ζ=0.3, 1.0, 2.0 (ωn=1.0)のとき、

%2次系のステップ応答,ζ依存性
clf

%ωn=1.0,ζ=0.3,時間=20sec,データ数=1000のとき
[y,t]=step(tf([1.0^2],[1 2*0.3*1.0 1.0^2]), 1, 20, 1000);
plot(t,y,"1")
legend("zeta=0.3")
hold on;

%ωn=1.0,ζ=1.0,時間=20sec,データ数=1000のとき
[y,t]=step(tf([1.0^2],[1 2*1.0*1.0 1.0^2]), 1, 20, 1000);
plot(t,y,"2")
legend("zeta=1.0")
hold on;

%ωn=1.0,ζ=2.0,時間=20sec,データ数=1000のとき
[y,t]=step(tf([1.0^2],[1 2*2.0*1.0 1.0^2]), 1, 20, 1000);
plot(t,y,"3")
legend("zeta=2.0")
hold on;

%x軸=0～20,y軸=0～1.4
axis([0 20 0 1.4])
xlabel("time(sec)")
%ylabel("")
title("Step Responce (omega_n = 1.0)")
grid;

%pngファイルに保存
print -dpng step1.png



②ωn=0.5, 1.0, 2.0 (ζ=0.3)のとき、

%2次系のステップ応答,ωn依存性
clf

%ωn=0.5,ζ=0.3,時間=20sec,データ数=1000のとき
[y,t]=step(tf([0.5^2],[1 2*0.3*0.5 0.5^2]), 1, 20, 1000);
plot(t,y,"1")
legend("omega_n=0.5")
hold on;

%ωn=1.0,ζ=0.3,時間=20sec,データ数=1000のとき
[y,t]=step(tf([1.0^2],[1 2*0.3*1.0 1.0^2]), 1, 20, 1000);
plot(t,y,"2")
legend("omega_n=1.0")
hold on;

%ωn=2.0,ζ=0.3,時間=20sec,データ数=1000のとき
[y,t]=step(tf([2.0^2],[1 2*0.3*2.0 2.0^2]), 1, 20, 1000);
plot(t,y,"3")
legend("omega_n=2.0")
hold on;

%x軸=0～20,y軸=0～1.4
axis([0 20 0 1.4])
xlabel("time(sec)")
%ylabel("")
title("Step Responce (zeta = 0.3)")
grid;

%pngファイルに保存
print -dpng step2.png

App Storeでランキングのダブり

なぜか、App Storeのランキングで25位と26位に、Google Earthがダブっていた。記録に残しておく。